Chemistry is all about bonds. Water is an oxygen atom bonded to two hydrogen atoms. The method of the bonding and the structure of the molecule are all dictated by the electrons.
Needless to say, simulating how atoms interact has been the backbone of my research. And it does take you to some interesting topics, such as what is even a bond? (This is a deep theoretical question given that there are many types of bonds, and that the bond between two atoms, such as oxygen and hydrogen, is unique to molecule and the material that particular bond is in e.g. the O-H bond in water and the O-H bond in ethanol are similar, but not the same).
Now you might say, "Hey, bonding is governed by electrons, and they are particles governed by quantum mechanics, so shouldn't we be simulating these bonds by solving Schrodinger's equations?" And you would be right. However, in the early days of simulations of chemistry, computers were big, bulky, and nowhere near powerful enough to solve even the quantum mechanical formula for water. An alternative was needed. That alternative is molecular mechanics, or force fields.
Molecular mechanics takes a different approach. We can observe using a variety of spectroscopy methods the motion of atoms and the structure of materials. And it is these results that can inform us as to the mathematical formula that describes the interaction between atoms. We call this empirical force field design. We know the results, we just need to fit the parameters of the formula to get the same (or at least close to) the results.
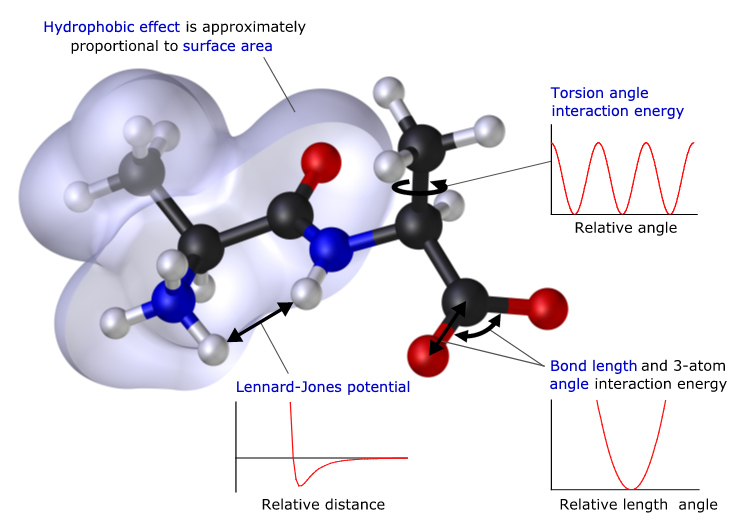
Now, fortunately, we know a few things about our atoms: we can measure the charges on atoms and molecules; we know the mass of atoms; we know the preferred geometrical arrangement of the atoms in a molecule; we know the typical bond lengths in molecules.
Ultimately early simulations of molecules used the concept of balls on springs, and fitted the parameters to reproduce the expected frequency of vibration of those bonds, as measure using infra-red spectroscopy. Pretty simple maths really. And that is the point. Many of the formula used are well known mechanical formula for describing balls at two ends of a spring. The spring has a force constant, and an "at rest" bond length. We know our molecules have to have a balanced charge, and dipoles and quadrupoles, and so again, we can tweak the charges of the atoms to reproduce these properties (though this is not always easy, and water is a great example of this). We can also describe the force constant that describes the interaction of two atoms bonded to the same atom, and how that angle flexes and vibrates. And we can also measure and thus model the way bonds, and thus the functional groups at either end of the bond, rotate around. All of the above can be done using simple Newtonian mechanics. For the early days of computing, there was an advantage to this too. Many of the functional forms used to describe bonding were harmonic in nature, or used other mathematical relationships to describe bonding, also had well developed computational algorithms so that they could be solved quickly and routinely on the computers of the time.
However, there are limits. Fitting a force field is a bit of a black art. You can overfit a force field to a particular set of reference data, which then hinders the use of the force field for other examples of the bond in other systems. There is also the fact that some properties are not captured, but which are important to how these molecules and atoms interact. This can lead us down the path of adding correction after correction to the simulation, layering mathematical formula on top of the original model, and making the entire fitting process hard to understand.
Of course, that is not to say that such models, even today, do not provide useful results. We still routinely use models designed in this way to perform many thousands of simulations if we are searching a chemical space, or very long, very larger simulations. And these are typically the scenarios where using quantum mechanical simulations is not viable given the relative computational expense of such methods. Next time I will give an overview of what we mean by quantum mechanical simualtions.

Comments